力学基础知识点

材料的力学性能

材料的力学性能是指材料在外力（如载荷、温度变化等）作用下表现出的变形和破坏特性。这些性能是材料设计和工程应用中的核心参数，直接影响材料的使用寿命、安全性和可靠性。

1. 强度/ \(Strength\)

定义： 强度是指构件抵抗破坏的能力，或材料抵抗永久变形或断裂的能力。

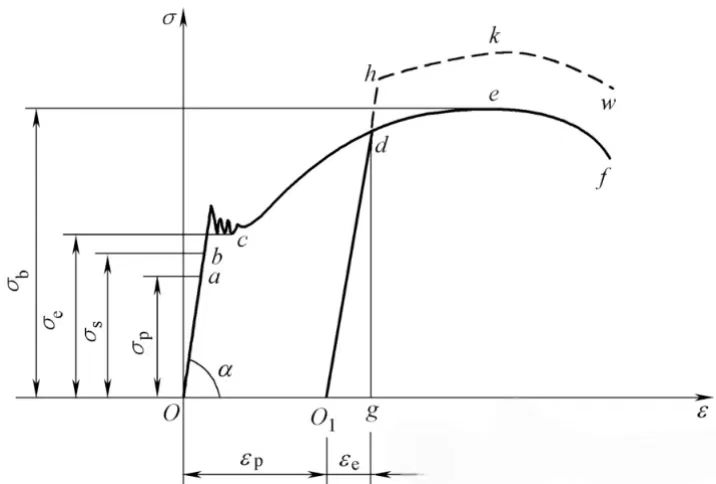
Fig. 1 应力-应变曲线

性能参数： 屈服强度（\(Yield\) \(Strength\)）： 对于无明显屈服的金属材料，规定以产生0.2%残余变形的应力值为其屈服极限。通常就把下屈服极限称为屈服强度。上图\(δ_{e}\)为材料的屈服强度。

抗拉强度（\(Tensile\) \(Strength\)）： 表示材料对最大均匀塑性变形的抗力，材料在拉伸破坏之前能承受的最大应力。上图\(δ_{b}\)为材料的抗拉强度。

2. 刚度/ \(Stiffness\)

定义： 刚度是材料或结构在外力作用下抵抗弹性变形的能力。

性能参数： 刚度越高，材料在相同外力下的变形越小。刚度与材料的弹性模量密切相关，弹性模量是材料本身的属性，反映其内在抗变形能力。

类型： 刚度根据变形模式可分为拉伸刚度、弯曲刚度、剪切刚度、扭转刚度。

3. 挠度/ \(Deflection\)

定义： 挠度指结构构件（如梁、板等）在外力（荷载）作用下发生的弹性位移。例如，桥梁在车辆经过时会向下弯曲，这种弯曲的垂直位移即为挠度。

物理意义： 挠度反映了结构的刚度：刚度越大，抵抗变形的能力越强，挠度越小。

4. 延伸率/ \(Elongation\)

定义： 延伸率指材料在拉伸断裂后，标距部分的伸长量与原标距长度的百分比，计算公式为：

\[ \delta=\frac{L_{f}-L_{0}}{L_{0}}{100\%} \]

其中，

\[ L_{f} 为原始标距长度， \]

\[ L_{0} 为断裂后标距长度。 \]

应用： 反映材料整体延展性，适用于评估材料在均匀变形阶段的塑性能力。

5. 断面收缩率/ \(Reduction\) \(of\) \(Area\)

定义： 断面收缩率指材料断裂后，横截面积减少量与原面积的百分比，计算公式为：

\[ \Psi=\frac{A_{0}-A_{f}}{A_{0}}{100\%} \]

其中，

\[ A_{0} 为原始横截面积， \]

\[ A_{f} 为断裂后最小横截面积。 \]

应用： 反映材料局部塑性变形能力，尤其在颈缩阶段的性能。

6. 泊松比/ \(Poisson's\) \(ratio\)

·定义： 泊松比是指材料在单向受拉或受压时，横向正应变与轴向正应变的比值；也叫横向变形系数，它是反映材料横向变形的弹性常数。

·公式： 杆件受拉伸或压缩载荷，应力不超过比例极限时，横向应变\(\varepsilon\)\(\prime\)与轴向应变\(\varepsilon\)之比的绝对值是一个常数，可表示为：

\[ \nu=-\frac{\epsilon_{横向}}{\epsilon_{纵向}} \]

由于横向应变与纵向应变符号相反（如拉伸时纵向伸长、横向收缩），公式中引入负号使泊松比为正值。

物理意义泊松比反映了材料在受力时的多维变形特性：

\[ \nu≈0.5:材料近似不可压缩(如橡胶)，体积几乎不变(横向收缩显著)。 \]

\[ \nu≈0：材料在拉伸/压缩时横向几乎不变形(如软木塞)。 \]

\[ \nu<0(拉胀材料)：拉伸时横向膨胀，具有特殊结构(如蜂窝材料)，应用于减震、吸能等领域。 \]

7. 弹性/ \(Elasticity\)

定义： 材料在卸载后恢复原始形状的能力。

核心指标： 弹性极限（材料能完全恢复的最大应力）。

特点： 弹性变形可逆（如橡皮筋拉伸后回弹）。

8. 韧性/ \(Toughness\)

定义： 材料在断裂前吸收能量的能力（需兼具强度与塑性）。

核心指标： 冲击韧性（单位体积吸收的能量）、断裂韧性（抗裂纹扩展能力）。

特点： 韧性好的材料抗冲击（如防弹玻璃），脆性材料（如陶瓷）反之。

应用： 安全头盔、防撞结构需高韧性。

9. 刚性/ \(Rigidity\)

定义： 结构整体抵抗变形的能力，结合材料刚度和几何形状（如截面尺寸）。

特点： 与刚度不同，刚性强调结构的综合抗变形能力（如铝梁加粗截面可提升刚性）。

应用： 建筑框架需高刚性以维持整体稳定性。

10. 塑性/ \(Plasticity\)

定义： 材料在超过弹性极限后发生永久变形而不断裂的能力。

核心指标： 延伸率（拉伸后长度变化百分比）、断面收缩率。

特点： 塑性变形不可逆（如金属冲压成型）。

应用： 金属加工（锻造、冲压）依赖塑性。

应力介绍

应力（\(Stress\)）： 是材料力学中的核心概念，表示单位面积上材料内部抵抗变形的力。通过系统分析应力状态并结合适当强度理论，可有效预测材料在复杂载荷下的失效行为，为工程设计提供依据。

1. 应力/\(Stress\)

【1】定义： 应力是物体在外力作用下，内部单位面积上产生的内力。

【2】物理意义: 它反映了材料在受力时的内部响应，是材料是否发生破坏或变形的重要指标。

【3】应力的概念： 在受力构件的某截面\(C\)上任取一点\(P\)，围绕该点取微小面积\(ΔS_{c}\)。

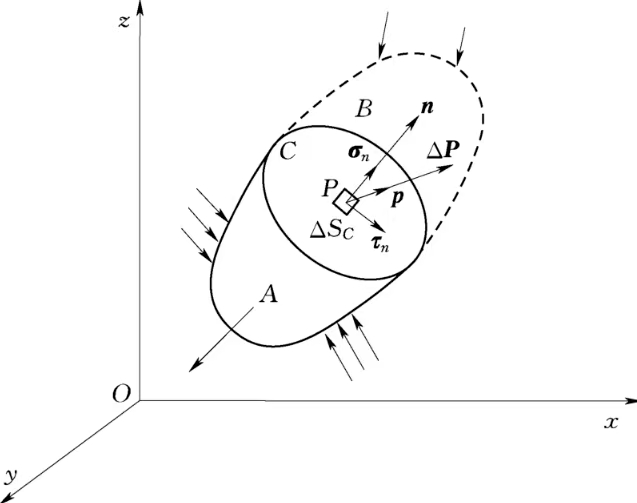
Fig. 2 应力示意图

假设\(ΔS_{c}\)上分布内力的合力为\(ΔP\)，其大小和方向与\(P\)点的位置有关。定义\(ΔS_{c}\)范围内单位面积上内力的平均集度为：

\[ p=\lim_{ΔS_{c}\to 0} \frac{ΔP}{ΔS_{c}} \]

平均内力集度\(p\)称其为点\(P\)的应力（\(stress\)），反映了内力在点\(P\)的强弱程度，%材料的强度分析主要是对应力进行计算。过\(P\)点的截面\(C\)是任意的，这样的截面有无穷多个，所有这些截面上应力的集合称为\(P\)点的应力状态。

2. 正应力和切应力
【1】应力
正应力： 将应力\(p\)分解为沿截面法向的分量\(σ_{n}\)，称为正应力/\(Normal\) \(Stress\)。
切应力： 将应力\(p\)分解为沿截面切向的分量\(τ_{n}\)，称为切应力/\(Shear\) \(Stress\)。

正应力和切应力是应力的两个分量

正应力：

\[ σ_{n}=\lim_{ΔS_{c}\to 0} \frac{ΔP_{n}}{ΔS_{c}} \]

切应力：

\[ τ_{n}=\lim_{ΔS_{c}\to 0} \frac{ΔP_{s}}{ΔS_{c}} \]

【2】方向与符号约定：
正应力： 拉应力为正，压应力为负。如拉伸金属棒时，截面产生拉应力；受压柱体内部为压应力。
切应力： 方向由截面取向和受力方向决定，通常遵循右手法则。如剪刀剪切纸张时，刀刃接触面产生切应力。

【3】区别与联系：

特征	正应力	切应力
方向	垂直于截面	平行于界面
主要诱因	轴向力、弯矩	剪切力、扭矩
材料破坏	脆性材料易拉断/压溃	延性材料易屈服/剪切滑移
典型公式	\(σ=\frac{F}{A}\)	\(τ=\frac{F}{A}\)(均匀分布)
应力状态	单轴、弯曲	纯剪切、扭转

【4】工程应用
·组合应力： 实际结构中常同时存在正应力和切应力（如梁的弯曲与剪切、组合），需通过应力张量分析。

·强度理论：
① 最大正应力理论适用于脆性材料（如铸铁）。
② 最大切应力理论（Tresca）适用于延性材料（如钢材）。

·应力集中： 几何突变处（如孔洞、缺口）会显著提高局部应力，需在设计时考虑。
正应力与切应力是材料力学的基础概念，分别对应垂直与切向的受力状态。理解它们的产生条件、计算方式及对材料行为的影响，是结构设计和强度分析的核心。实际应用中需结合具体载荷类型（拉压、剪切、弯曲、扭转）进行综合分析。

3. 主应力和主平面

【1】应力状态: 通过某一点可以作无数个不同方位的截面，这些截面上的应力情况就称为一点的应力状态。
研究一点的应力状态，称为应力分析。理论分析已经证明，在过受力构件中一点的所有截面中，只要有三个正交面上的应力是已知的，则所有其他截面上的应力都能确定。

【2】主平面与主应力：
主平面： 单元体上没有切应力的面称为主平面。
主应力： 主平面上的正应力称为主应力。

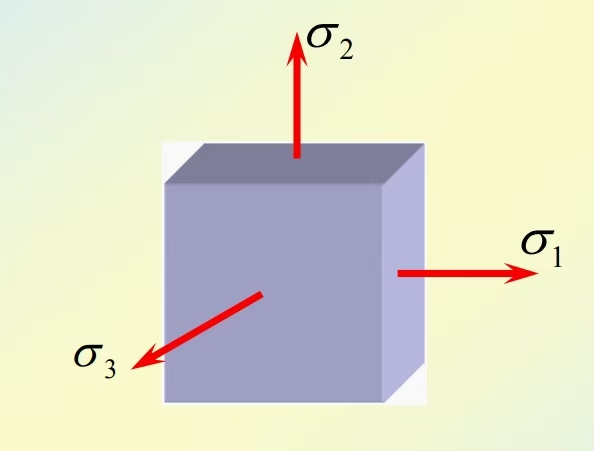
Fig. 3 主应力示意图

在受力构件内的任意点总可以找到三个互相垂直的主平面，因此总存在三个互相垂直的主应力，通常用\({σ_{1}}\)、\({σ_{2}}\)、\({σ_{3}}\)表示，规定\({σ_{1}}\)、\({σ_{2}}\)、\({σ_{3}}\)按代数值大小排列，即\({σ_{1}}\)≥\({σ_{2}}\)≥\({σ_{3}}\)。

主应力有三个分量，分别是：
① 最大主应力/σ1：指作用在某一方向上最大的正应力。
② 中间主应力/σ2：是作用在与最大和最小主应力方向垂直的方向上的应力。
③ 最小主应力/σ3：指作用在某一方向上的最小正应力。

主应力方向即是材料中应力最大的方向（\({σ_{1}}\)）、最小的方向（\({σ_{3}}\)）以及中间方向（\({σ_{2}}\)），这三个方向相互垂直且称为应力主轴。

【3】物理意义: 主应力反映了材料内部某点的最大拉压应力状态，是判断材料是否发生屈服或断裂的重要依据。

4. 等效应力

【1】定义
等效应力是材料力学中的一个标量值，用于将复杂多轴应力状态（如拉伸、压缩、剪切等组合作用）简化为一个等效的单轴应力值。

等效应力在材料力学的第四强度理论（畸变能密度理论）中引入，该理论认为：畸变能密度是引起屈服流动破坏的主要因素，其计算公式为：

\[ \sqrt{\frac{1}{2}[({σ_{1}}-{σ_{2}})^2+({σ_{2}}-{σ_{3}})^2+({σ_{3}}-{σ_{1}})^2]}\leq[σ] \]

【2】等效应力性质
① 等效应力与空间坐标轴的选取无关。根据公式，只与应力偏量的第二不变量\({J_{2}}\)有关，与空间坐标轴的选取无关。
② 叠加一个静水应力状态不影响等效应力的数值。静水应力可用应力球张量表示，而应力偏量的第二不变量\({J_{2}}\)与应力球张量无关。
③ 主应力全反号时，数值不变。因此等效应力适用于拉压性能相同或相近的材料。

【3】物理意义
等效应力的理论基础是畸变能密度理论（第四强度理论），认为材料的屈服与形状改变能（畸变能）相关，而非体积变化。
第四强度理论认为不论什么材料、也不管材料处于什么应力状态，只要畸变能密度\({υ_{d}}\)达到与材料性质有关的某一极限值，则材料就发生屈服。
等效应力是工程分析中的核心工具，将复杂应力状态简化为直观的标量值，帮助快速判断结构安全性。实际应用中需结合材料特性、工况和安全系数综合评估。

##应变介绍

在材料力学和连续介质力学中，应变是用来描述物体内部质点之间相对位移导致的局部变形程度的物理量。 也就是说，它衡量的是物体在受到外力作用时，其形状或尺寸发生了多大的相对变化。

应变是描述物体变形程度的度量尺。在工程领域它不仅是理解材料行为（应力-应变关系）的基础，更是贯穿设计、分析、试验、制造、监测全过程的核心参数。通过测量和分析应变有以下指导作用：

[1] 确保结构安全可靠（强度、刚度、稳定性）

[2] 优化设计（轻量化、高效化）

[3] 预测寿命（疲劳分析）

[4] 监控运行状态（结构健康监测）

[5] 精确测量物理量（传感器）

1.弹性应变与塑性应变

在基础材料力学中，变形可以用正应变和切应变进行量化。一个构件中应变的累积结果就是变形，如拉、弯或扭。材料在快速加载时表现出来的变形可分为弹性变形和塑性变形。

（a）弹性变形：研究材料在可恢复变形（卸载后恢复原状）的力学行为。

（b）塑性变形：研究材料在不可恢复变形（永久变形）阶段的力学行为，在卸载后不能恢复，因而是永久变形。

拉伸试验就是在单个轴向力作用下，缓慢拉动一个材料试样直至其发生断裂。由拉伸试验所获得的主要结果就是整个试验的工程应力-工程应变曲线图，称之为应力-应变曲线，如图@sec0.1-fig:Stress_strain所示。

有限元

在数学中，有限元法（\(FEM\)，\(Finite\) \(Element\) \(Method\)）是一种为求解偏微分方程边值问题近似解的数值技术。求解时对整个问题区域进行分解，每个子区域都成为简单的部分，这种简单部分就称作有限元。它通过变分方法，使得误差函数达到最小值并产生稳定解。

\(ABAQUS\)

\(ABAQUS\)是一套功能强大的工程模拟的有限元软件，其解决问题的范围从相对简单的线性分析到许多复杂的非线性问题。\(ABAQUS\)包括一个丰富的、可模拟任意几何形状的单元库。并拥有各种类型的材料模型库，可以模拟典型工程材料的性能，其中包括金属、橡胶、高分子材料、复合材料、钢筋混凝土、可压缩超弹性泡沫材料以及土壤和岩石等地质材料，作为通用的模拟工具，\(ABAQUS\)除了能解决大量结构（应力/位移）问题，还可以模拟其他工程领域的许多问题，例如热传导、质量扩散、热电耦合分析、声学分析、岩土力学分析（流体渗透/应力耦合分析）及压电介质分析。

.inp文件格式

1. 模型数据

模型数据用来定义一个完整的有限元模型。有一些模型数据是必需的，包括：

a）单元和节点数据：模型的几何形状是通过单元和节点来定义的，因此必须给出节点和单元信息；

b）材料：必须定义分析过程中需要用到的各种材料的性能。

还有一些模型数据不是必不可少的，例如：

a）部件和装配件：如果 INP 文件是由 Abaqus/CAE 自动生成的，将会包含部件（*PART）、装配件（*ASSEMBLY）、实体（*INSTANCE）等数据块；如果 INP 文件是由其他前处理器（例如 MSC.PATRAN、FEMAP 等）生成的，其结构将不包含部件、装配件和实体等数据块，而是直接定义节点和单元等数据信息；

b）初始条件：例如初始应力、初始温度、初始速度等；

c）边界条件、约束、相互作用、幅值、输出控制、读者子程序等。

2. 历程数据

a）历程数据包括分析类型、荷载、边界条件和输出要求等。有限元分析的目的是模拟模型对外部荷载或者初始条件的响应情况，因此一个完整的Abaqus有限元分析是建立在分析步基础上的，这些分析步都在历程数据中描述。

b）一个 INP 文件可以包含多个分析步，每个分析步都以 *STEP 开始，以 *END STEP 结束。*STEP 是历程数据和模型数据的分界点，第一个 *STEP 之前的所有内容均属于模型数据，其后的所有内容则都属于历程数据。

c）分析步的类型是必需的历程数据，它必须紧跟 *STEP 关键词。Abaqus中有两种分析步：一种是一般分析步（general step），可以是线性或非线性的；另一种是线形摄动分析步（linear perturbation step），只能是线性的。

还有一些历程数据不是必不可少的，包括：

a）载荷：定义载荷的类型和大小，它可以描述为时间的函数（即通过幅值曲线来定义）；

b）边界条件；

c）输出控制选项。

注意：

在书写 INP 文件时，模型数据必须位于历程数据之前，但是在模型数据和历程数据内部，数据块的顺序和位置一般是任意的，但是有一些情况例外，包括：

1）关键词 *HEADING 必须放在 INP 文件的第一行；

2）关键词 *ELASTIC、*DENSITY 和 *PLASTIC 是 *MATERIAL 的子选项，它们必须直接跟在 *MATERIAL 之后；

3）关键词 *STATIC、*DYNAMIC 和 *FREQUENCY 必须跟在 *STEP 之后，用来指定分析步对应的分析类型。

静力分析与动力学的区别

有限元分析中动力学（\(Dynamic\) \(Analysis\)）与静力学（\(Static\) \(Analysis\)）的本质区别源于二者对物理现象的描述方式、控制方程及求解策略的根本差异。

1. 物理区别

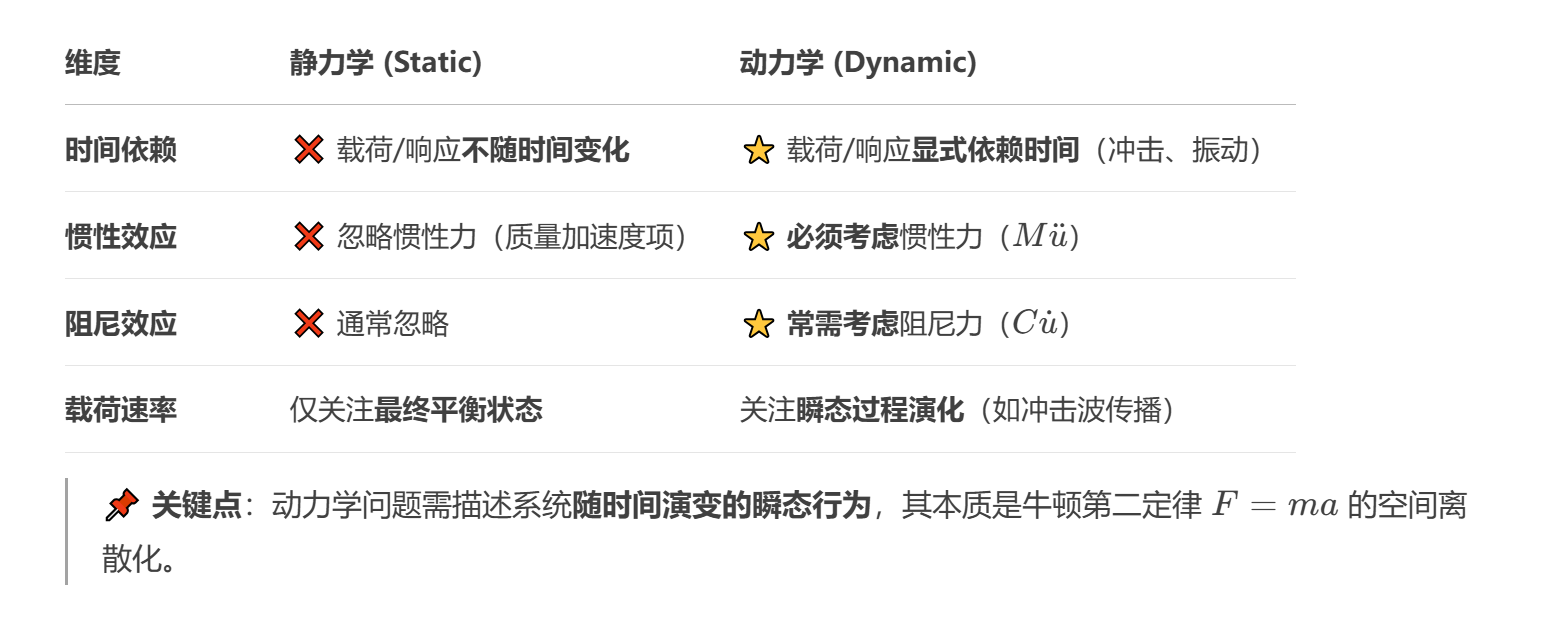
Fig. 4 物理本质区别

2. 控制方程对比

静力学方程

\[ [K]\{u\}=\{F\} \]

注释

\[ K：刚度矩阵 \]

\[ u：位移向量 \]

\[ F：静态载荷向量 \]

特点：线性代数方程，求解单一平衡状态。

动力学方程

\[ [M]\{\ddot u\}+[C]\{\dot u\}+[K]\{u\}=\{F(t)\} \]

\[ M：质量矩阵(新增项) \]

\[ C：阻尼矩阵(新增项) \]

\[ \ddot u,\dot u ：加速度/速度向量 \]

\[ F(t)：时间相关载荷 \]

特点：二阶常微分方程组，求解时间域响应历程。

注：符合运算大全 https://www.cnblogs.com/syqwq/p/15190115.html

3.求解方法差异

Fig. 5 求解方法的区别

4.本质区别总结

Fig. 6 本质区别

\(CalculiX\) \(CrunchiX\)

\(CalculiX\) \(CrunchiX\)是一款开源的有限元分析求解器（\(FEM\) \(solver\)），主要用于结构力学、热力学等场问题的数值模拟。专注于执行有限元模型的数值计算，支持线性与非线性分析，包括静态、动态及热力学问题。采用与商业软件\(Abaqus\)相似的输入格式，便于用户迁移现有模型。

安装\(CCX\)(\(Linux\)系统)

在\(Linux\)系统中\(FENGSim\)软件的安装和打开终端代码

    "下载"
    sudo apt install git
    git clone https://github.com/OpenDigitalTwin-Dev/FENGSim.git
    cd FENGSim/cli（文件路径，在终端直接打开）

    "安装和卸载"
    ./install.sh or ./uninstall.sh

    "打开"
    cd FENGSim/cli（文件路径）
    ./qtcreator.sh

在\(Linux\)系统中\(CalculiX\)软件的安装和打开终端代码

    "下载"
    cd FENGSim/toolkit/NSM/extern/Calculix 

    "安装和卸载"
    ./install.sh or ./uninstall.sh

    "打开算例Tubes算例"
    cd FENGSim/toolkit/NSM/extern/Calculix/examples/Contact/Tubes

    "求解计算"
    ./../../../bin/ccx_2.21 solve

    "后处理文件格式转化"
    python3 ./../../../ccx2paraview/ccx2paraview.py jobname.frd vtk(文件格式转换frd文件转化为vtk)

在\(Linux\)系统中后处理工具\(paraview\)的安装过程及其应用

    1、sudo pip3 install numpy
    2、sudo apt install python3-pip
    3、sudo pip3 install vtk
    4、sudo apt install paraview
    paraview或者paraview &（运行Paraview）

\(Tube\)算例\(Solve.inp\)文件注释

\(CCX\)生成的\(Solve.inp\)文件语句注释

** includes ##节点、网格、面等几何文件输入##

*include, input=all.msh ##模型的网格和节点编号信息文件##

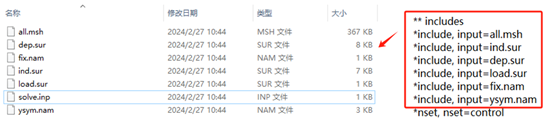
Fig. 7 节点、网格、面等信息示意图

##(*NODE, NSET=Nall 所有节以及节点的集合名称Nall)##

##(*ELEMENT, TYPE=C3D8I, ELSET=Eall 所有单元以及单元的集合名称Eall)##

*include, input=ind.sur ##主面的信息主要是单元编号，Sind主面名称##

##(**Surfaces based on ind *SURFACE, NAME=Sind 1（单元编号）, S1(面)…)##

*include, input=dep.sur ##从面的信息主要是单元编号，Sdep从面名称##

##(** Surfaces based on dep *SURFACE, NAME=Sdep 901（单元编号）, S2(面)…)##

*include, input=load.sur ##载荷的信息, 单元编号，Sload载荷名称##

*include, input=fix.nam ##固定约束信息, 节点编号,Nfix集合名称##

*include, input=ysym.nam ##对称约束的名称信息，节点编号，Nysym集合名称##

*nset, nset=control ##定义一个新的节点集合（nset），并命名为control###

1   ##节点编号为1的点并命名为control，下文中control 均为该节点##

**Constraints ##设置模型的约束条件##

*boundary
Nfix,1,3  ##节点集合Nfix中的所有节点在第一个、第二和第三个自由度（即X、Y、Z方向平动自由度）上施加固定约束##

Nysym,2  ##节点集合Nysym施加对称约束，关于y轴垂直面对称##

**Material ##材料##

*MATERIAL, NAME=Aluminium
*ELASTIC   ##弹性模量和密度##
70000, 0.34
*DENSITY
2.7e-9
*solid section, elset=Eall, material=Aluminium ##所有单元赋予材料属性##

**Contact ##接触分析##

*surface interaction, name=telescope  ##定义一个接触，命名为telescope##
*surface behavior, pressure-overclosure=linear  ##定义接触面之间的行为，使用了线性压力-间隙关系##
100000.   ##接触刚度参数##
*contact pair, interaction=telescope, type=surface to surface  ##定义接触对，交互名称为telescope，类型为表面到表面##
Sdep,Sind   ##指定接触对的从面Sdep和主面Sind##

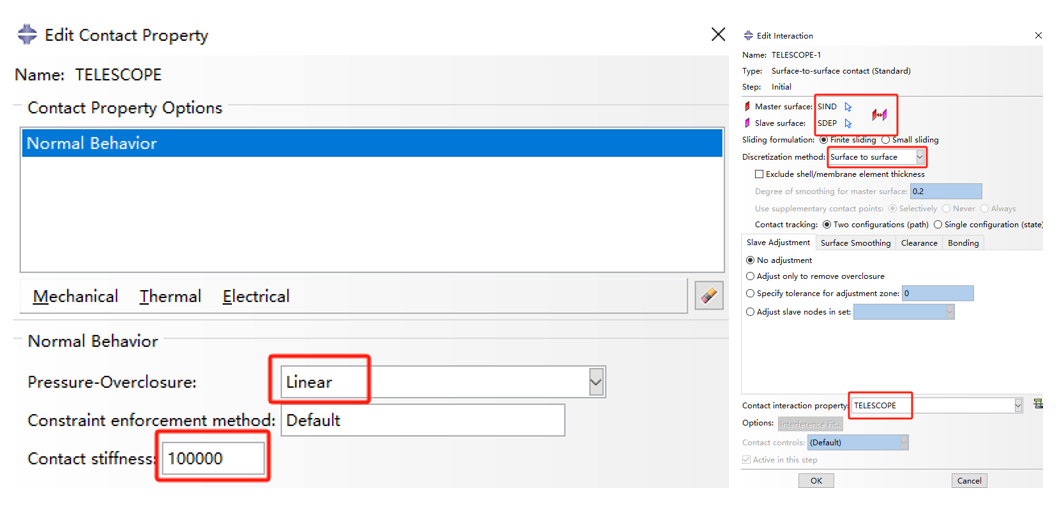
Fig. 8 静力学面-面接触参数设置

**Coupling ##耦合约束##

*coupling, ref node=1, surface=Sload, constraint name=c1    ##定义一个耦合约束，参考节点为1，耦合从面为Sload，约束名称为c1##
*kinematic   ###指定耦合的类型为运动学耦合，约束一组节点的所有的或者指定节点的自由度到参考点的刚体运动###
1   ##约束x方向##
3   ##约束z方向##
*boundary
control,1,2  ##约束参考点（节点）ref node在x和y方向的自由度##

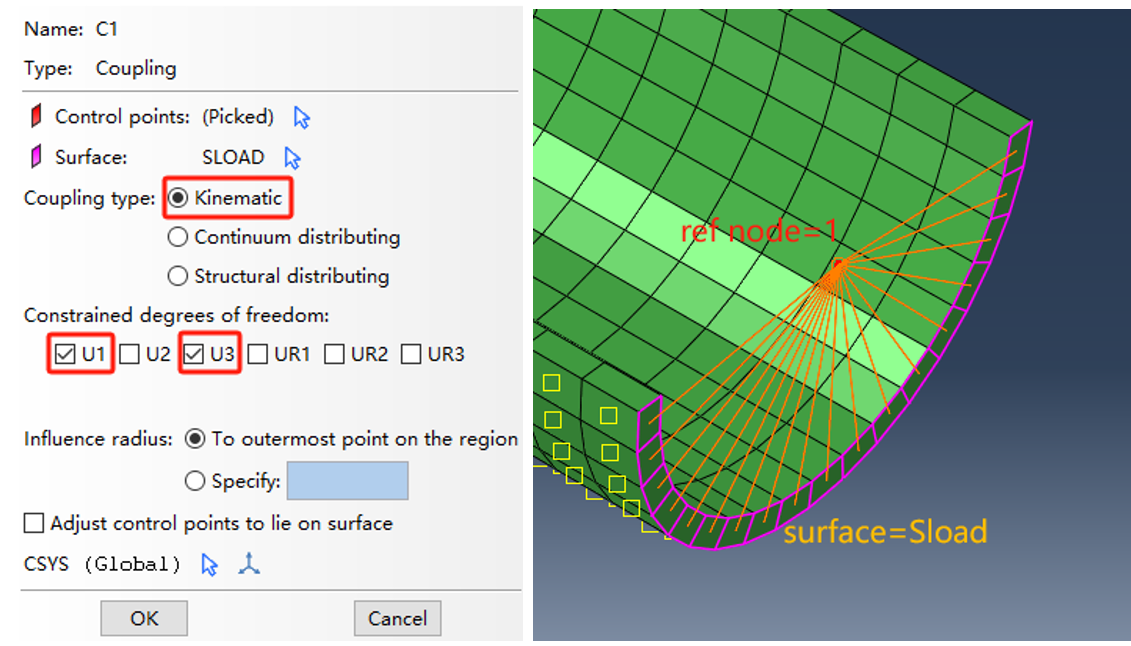
Fig. 9 耦合参数以及效果展示图

**Step ##分析步##

*step,nlgeom  ##定义一个包含非线性几何效应的分析步骤##
*static  ##静态分析##
0.1,1  ##表示初始时间增量为0.1，总步长时间为1 ##
*boundary
control,5,5,0.3  ##约束参考点（节点集）ref node在UR2方向旋转0.3弧度##

**Output ##输出##

*NODE FILE  ##节点（Node）的信息，节点是构成有限元模型的几何点##
U  ##节点的位移（U-displacement）信息##
*el file
S  ##应力（Stress）信息##
*section print, surface=Sload,name=sp1  ##这是一个输出请求，用于指定在分析结果中的特定部分的信息。这里指定了表面（surface）Sload的结果信息，并且给这个输出请求命名为sp1##
SOM  ##abaqus中没有定义，ccx中指section moments 截面弯矩##
*contact file  ##保存接触应力的文件##
CSTR  ## abaqus中没有定义，ccx中指contact stress 接触应力##
*END STEP ##当前步骤（STEP）的结束##

两款软件的运行计算结果如下，最大位移基本一致，最大应力出现位置是一致的，但是最大值有较大差距。

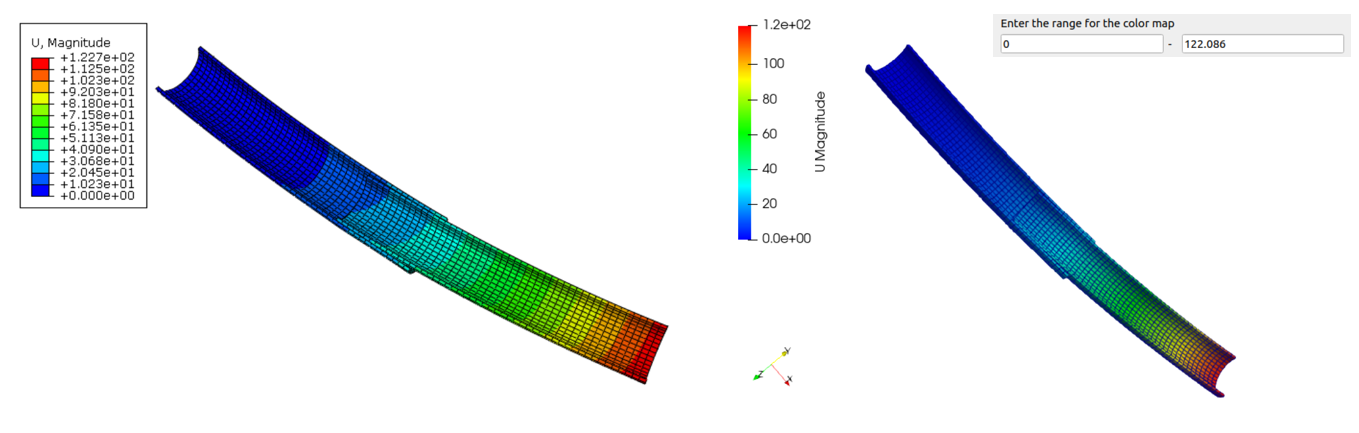
Fig. 10 Tube算例位移云图（左ABAQUS,右CCX）

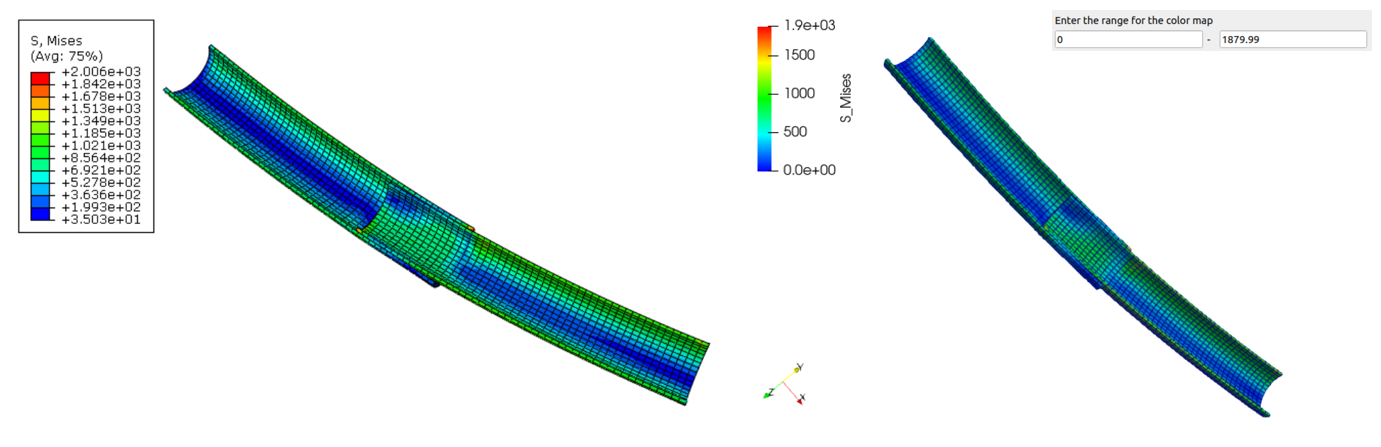
Fig. 11 Tube算例应力云图（左ABAQUS,右CCX）

\(ABAQUS\)与\(CCX\)算例计算结果对比

算例：几何尺寸：边长10mm的立方体，材料属性：密度1，弹性模量210，泊松比0.3。塑性：0.24，0。载荷：一端固支，另一端拉伸\(1mm\)。

1. 静力学+线弹性

位移云图对比

Fig. 12 位移云图（静力、线弹性）

应力云图对比

Fig. 13 应力云图（静力、线弹性）

2. 显示动力学+线弹性

位移云图对比

Fig. 14 位移云图（显示动力学、线弹性）

应力云图对比

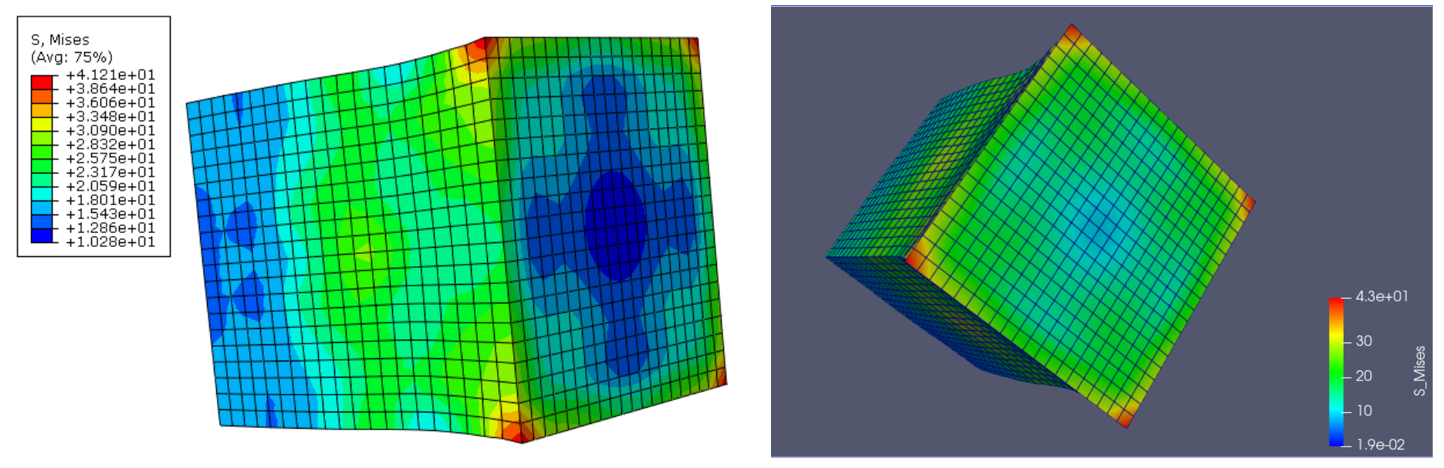
Fig. 15 应力云图（显示动力学、线弹性）

3. 显示动力学+塑性

位移云图对比

Fig. 16 位移云图（显示动力学、弹塑性）

应力云图对比

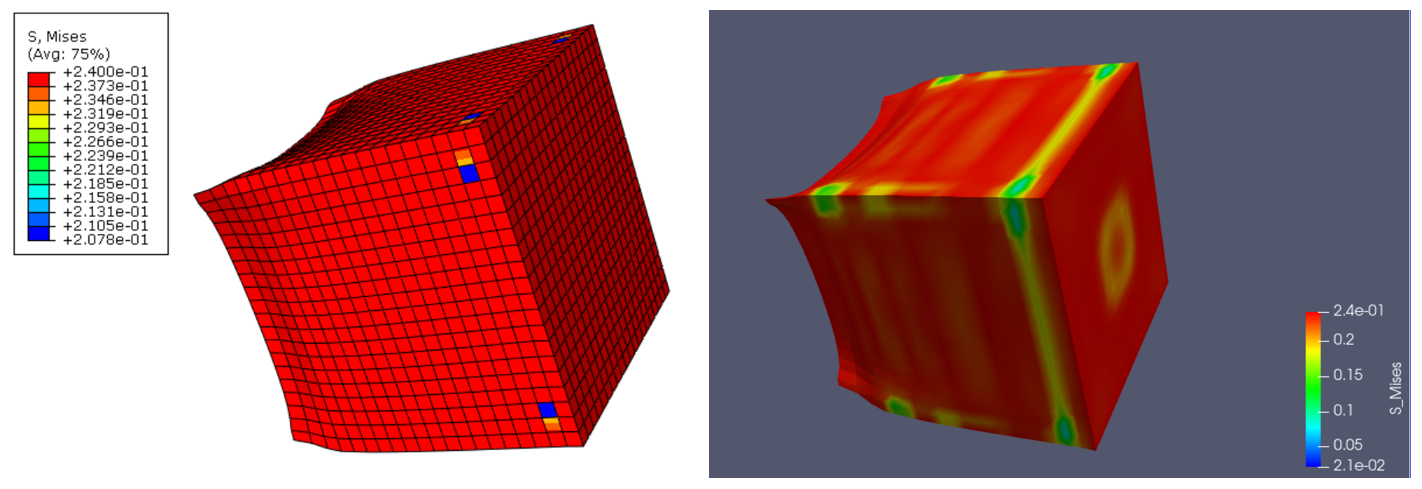
Fig. 17 应力云图（显示动力学、弹塑性）

4. 显示动力学+塑性+几何非线性

位移云图对比

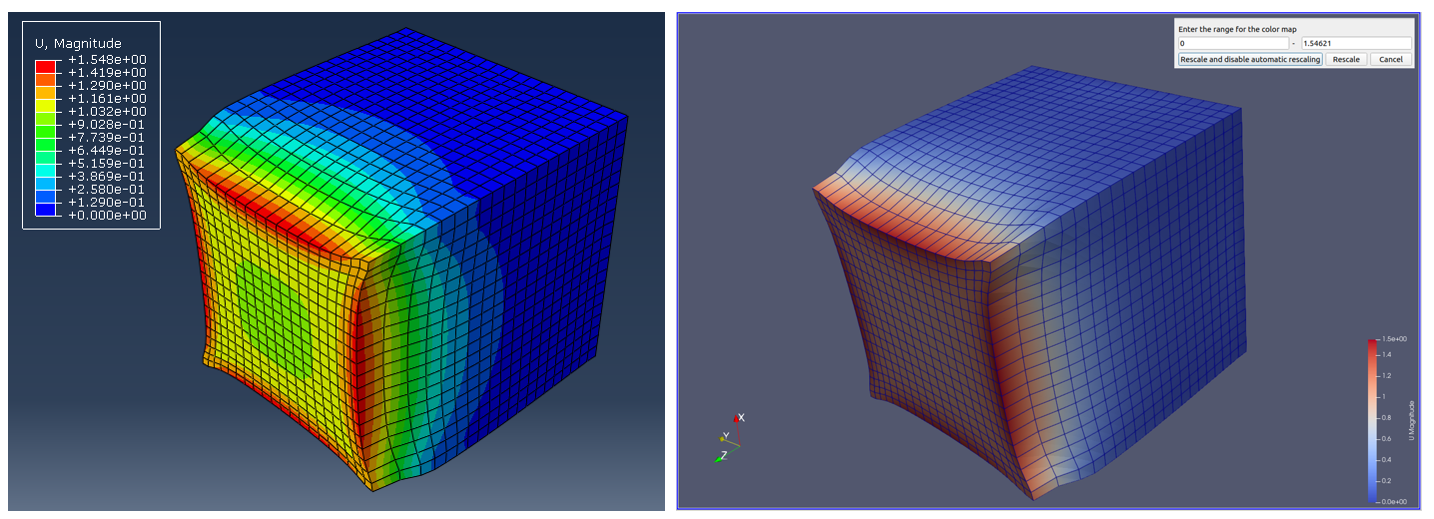
Fig. 18 位移云图（显示动力学、弹塑性、几何非线性）

应力云图对比

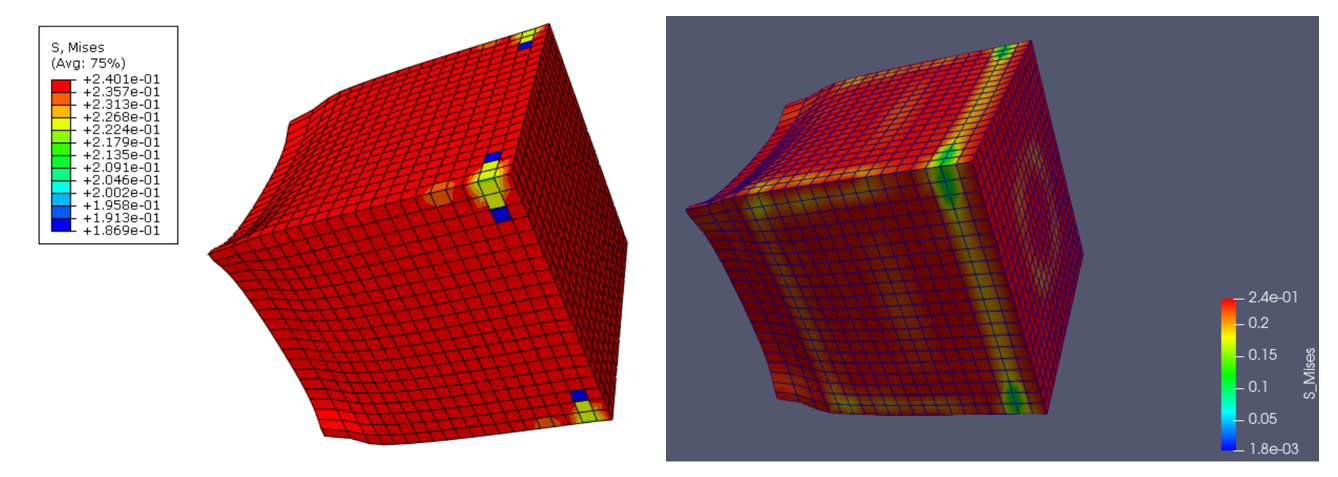
Fig. 19 应力云图（显示动力学、弹塑性、几何非线性）

CCX中的刚体定义

刚体定义参考算例（Biegung），以实体单元为基准，根据相应语句进行刚体定义（具体细节如下）。

*include, input=rmov.nam （包含节点和网格信息 *NSET,NSET=Nrmov，*ELSET,ELSET=Ermov ）
*include, input=rfix.nam
*include, input=ref.nam 
*NSET,NSET=Nref 
1,
*include, input=rot.nam
*NSET,NSET=Nrot 
2, 
……
*solid section, elset=Ermov, material=tool
……
*boundary
Nref, 1,3
Nrot, 1,3
……
*rigid body, nset=Nrmov, ref node = 1 , rot node = 2
……
*boundary
Nrot,2,2,1.57

注：CCX中算例中有刚体定义的.inp文件，导入到ABAQUS中运行，定义刚体的语句会报错，需要做相应的修改。

ABAQUS中在相互作用模块中定义刚体，具体语句如下（与CCX比较相似）：

**Constraint
*Rigid Body, ref node=1320, elset=Semi-cylinder

在ABAQUS中运行Biegung算例需要对inp文件做如下修改：
** rigid body
*rigid body, ELSET=Ermov ,  REF NODE = Nrot 
*rigid body, ELSET=Erfix , REF NODE = Nref

注：边界条件也要做出相应的修改，看具体分析修改。

算例Biegung信息如下图所示

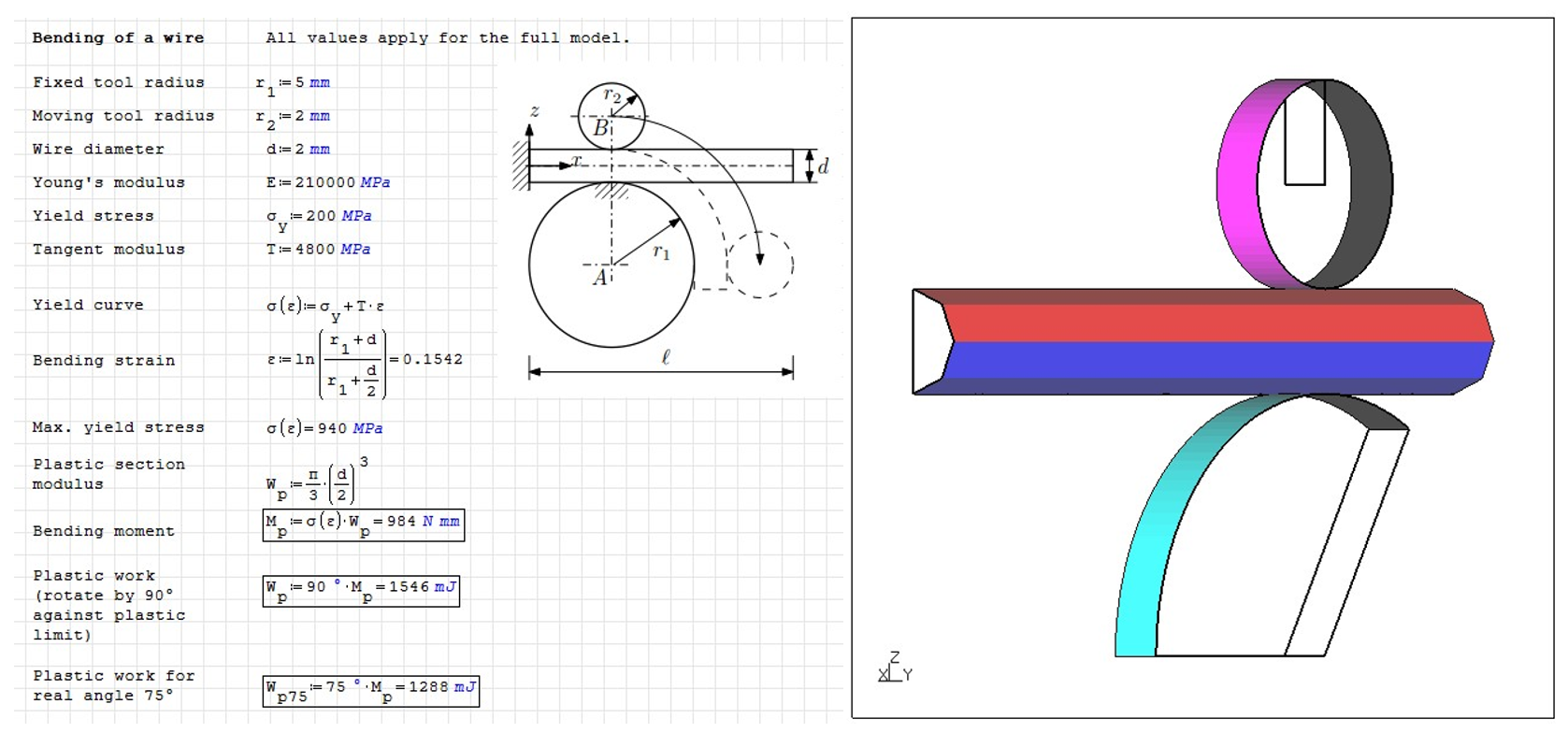
Fig. 20 算例参数及模型

算例Biegung计算结果对比(Static Nlgeom)

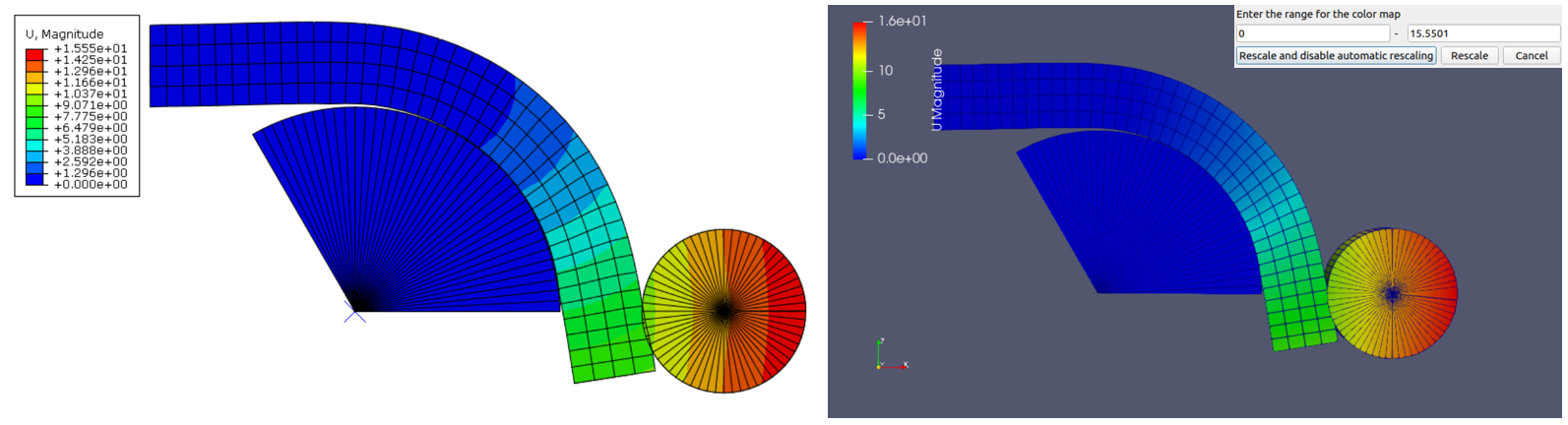
Fig. 21 位移云图（左ABAQUS,右CCX）

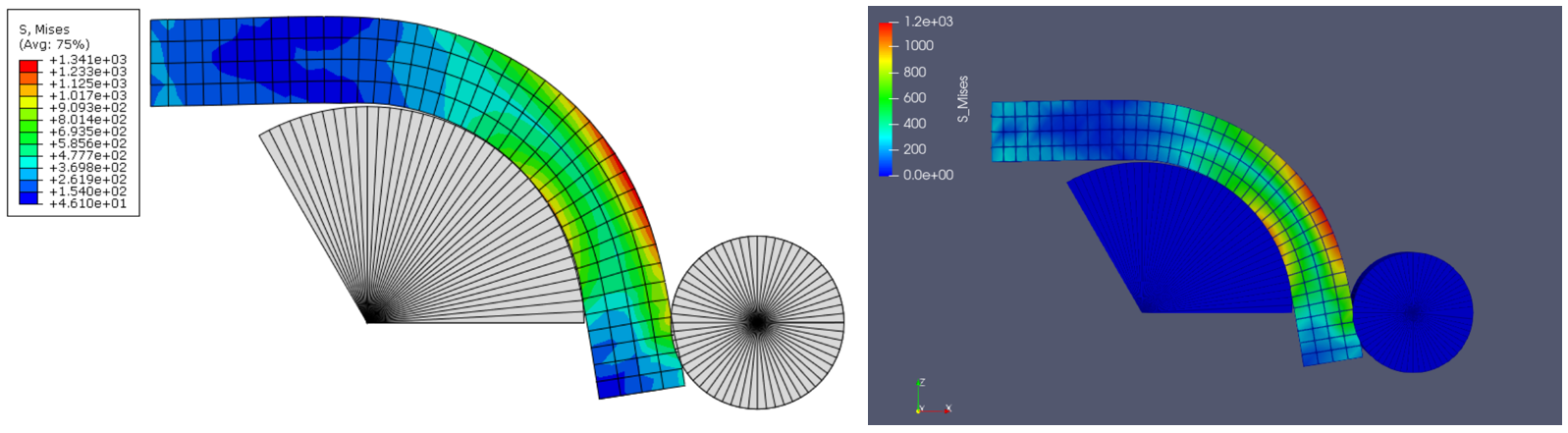
Fig. 22 应力云图（左ABAQUS,右CCX）

由上图可知，计算结果中的最大应力并不是一致的。

修改接触类型：node to surface <修改为> surface to surface，ABAQUS就算结果如下，最大应力值相差266MPa。然而CCX计算时报错”*ERROR: too many cutbacks”无结果。

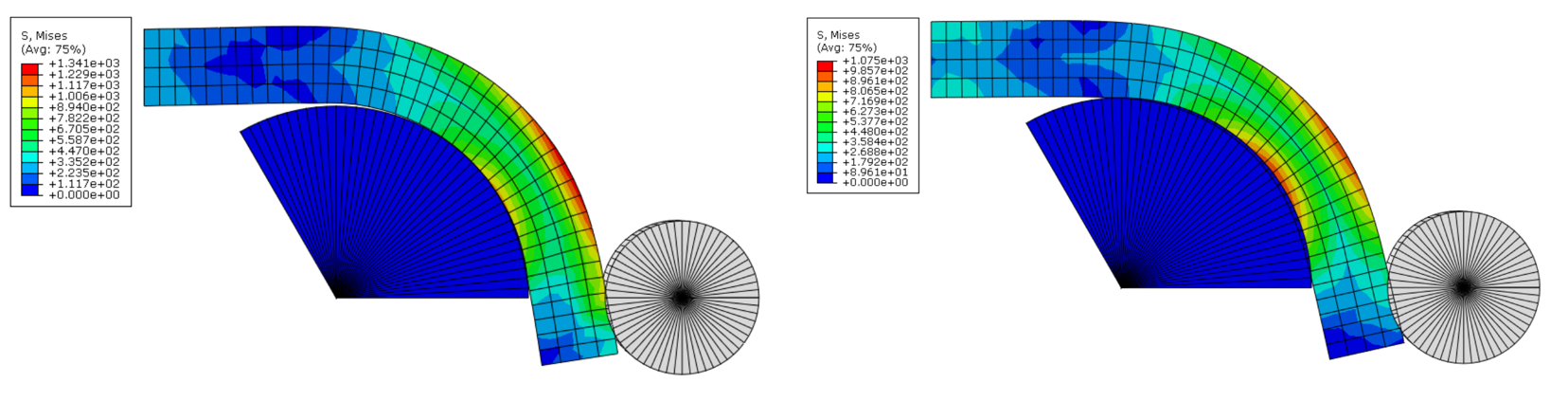
Fig. 23 应力云图（左node to surface,右surface to surface）

It will be rendered in a special box when you build your book.

Here is an inline directive to refer to a document: Notebooks with MyST Markdown.

Citations

You can also cite references that are stored in a bibtex file. For example, the following syntax: {cite}`holdgraf_evidence_2014` will render like this: [HdHPK14].

Moreover, you can insert a bibliography into your page with this syntax: The {bibliography} directive must be used for all the {cite} roles to render properly. For example, if the references for your book are stored in references.bib, then the bibliography is inserted with:

[HdHPK14]

Christopher Ramsay Holdgraf, Wendy de Heer, Brian N. Pasley, and Robert T. Knight. Evidence for Predictive Coding in Human Auditory Cortex. In International Conference on Cognitive Neuroscience. Brisbane, Australia, Australia, 2014. Frontiers in Neuroscience.

Learn more

This is just a simple starter to get you started. You can learn a lot more at jupyterbook.org.

123